1514. Path with Maximum Probability

⭐️⭐️⭐️

# 題目敘述

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i] .

Given two nodes start and end , find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end , return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

# Example 1

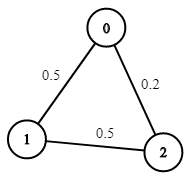
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

# Example 2

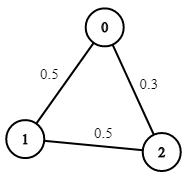
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

# Example 3

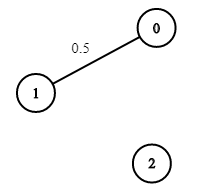
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.

# 解題思路

# Solution

class Solution {

    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {

        double[] maxProb = new double[n];

        maxProb[start] = 1.0;

        for (int i = 0; i < n - 1; i++) {

            boolean hasUpdate = false;

            for (int j = 0; j < edges.length; j++) {

                int u = edges[j][0];

                int v = edges[j][1];

                double pathProb = succProb[j];

                if (maxProb[u] * pathProb > maxProb[v]) {

                    maxProb[v] = maxProb[u] * pathProb;

                    hasUpdate = true;

                }

                if (maxProb[v] * pathProb > maxProb[u]) {

                    maxProb[u] = maxProb[v] * pathProb;

                    hasUpdate = true;

                }

            }

            if (!hasUpdate) {

                break;

            }

        }

        return maxProb[end];

    }

}