⭐️⭐️⭐️⭐️⭐️
# 題目敘述
You have an undirected, connected graph of n nodes labeled from 0 to n - 1 . You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.
Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
# Example 1
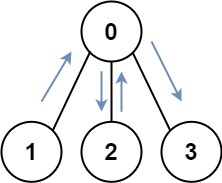
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]
# Example 2
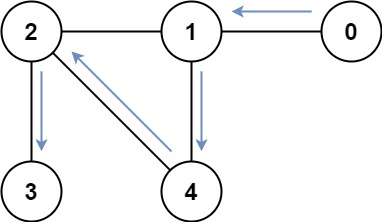
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]
# 解題思路
Use BitMask + BFS
運算式介紹:
allVisitedMask = (1 << n) - 1: 運算結果為15,以二進位來查看為1111,用於表示全部節點都走過了。currMask: 表示當前queue中經過了那些節點。newMask = currMask | (1 << next): 表示經過下一個node(next) 後的所有經過節點,|運算子稱作OR,運算方式如:0011 | 0101 = 0111。
BFS 結束條件:
- 如果經過相同
node(newMask),且下一個去向也是相同node(next),visited[newMask][next] == true,可以不用再跑下去。 - 如果
currMask == allVisitedMask表示所有節點都走過了,而currLen - 1就是答案。
# Solution
import java.util.Arrays; | |
import java.util.LinkedList; | |
import java.util.Queue; | |
class Solution { | |
public int shortestPathLength(int[][] graph) { | |
int n = graph.length; | |
int allVisitedMask = (1 << n) - 1; | |
Queue<int[]> queue = new LinkedList<>(); | |
boolean[][] visited = new boolean[allVisitedMask + 1][n]; | |
for (boolean[] v : visited) { | |
Arrays.fill(v, false); | |
} | |
for (int currNode = 0; currNode < n; currNode++) { | |
int initialMask = (1 << currNode); | |
queue.add(new int[] { currNode, initialMask, 1 }); | |
visited[initialMask][currNode] = true; | |
} | |
while (!queue.isEmpty()) { | |
int[] curr = queue.poll(); | |
int currNode = curr[0]; | |
int currMask = curr[1]; | |
int currLen = curr[2]; | |
if (currMask == allVisitedMask) { | |
return currLen - 1; | |
} | |
for (int i = 0; i < graph[currNode].length; i++) { | |
int next = graph[currNode][i]; | |
int newMask = currMask | (1 << next); | |
if (visited[newMask][next]) { | |
continue; | |
} | |
queue.add(new int[] { next, newMask, currLen + 1 }); | |
visited[newMask][next] = true; | |
} | |
} | |
return -1; | |
} | |
} |
單字
** **
!! !!
片語 & 搭配詞
!! !!
